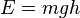Calculating the Amount of Available Power ~ Hydroelectric Energy

A simple formula for approximating electric power production at a hydroelectric plant is: $P = ρ h r g k$ , where

$P$ is Power in watts,
$ρ$ is the density of water (~1000 kg/m³),
$h$ is height in meters,
$r$ is flow rate in cubic meters per second,
$g$ is acceleration due to gravity of 9.8 m/s²,
$k$ is a coefficient of efficiency ranging from 0 to 1. Efficiency is often higher (that is, closer to 1) with larger and more modern turbines.

Annual electric energy production depends on the available water supply. In some installations the water flow rate can vary by a factor of 10:1 over the course of a year.

A hydropower resource can be measured according to the amount of available power, or energy per unit time. In large reservoirs, the available power is generally only a function of the hydraulic head and rate of fluid flow. In a reservoir, the head is the height of water in the reservoir relative to its height after discharge. Each unit of water can do an amount of work equal to its weight times the head.

The amount of energy, E, released when an object of mass m drops a height h in a gravitational field of strength g is given by

$\, E = mgh$

The energy available to hydroelectric dams is the energy that can be liberated by lowering water in a controlled way. In these situations, the power is related to the mass flow rate.

$\frac{E}{t} = \frac{m}{t}gh$

Substituting P for ^E⁄_t and expressing ^m⁄_t in terms of the volume of liquid moved per unit time (the rate of fluid flow, φ) and the density of water, we arrive at the usual form of this expression:

$P = \rho\, \phi\, g \, h$

A simple formula for approximating electric power production at a hydroelectric plant is:

P = hrgk

where P is Power in kilowatts, h is height in meters, r is flow rate in cubic meters per second, g is acceleration due to gravity of 9.8 m/s2, and k is a coefficient of efficiency ranging from 0 to 1. Efficiency is often higher with larger and more modern turbines.

Some hydropower systems such as water wheels can draw power from the flow of a body of water without necessarily changing its height. In this case, the available power is the kinetic energy of the flowing water.

$P = \frac{1}{2}\,\rho\,\phi\, v^2$